기초단계
실습2
x<-arima.sim(list(ma=0.7), n=100)
par(mfrow=c(2,1))
acf(x, main="ACF ")
pacf(x, main="PACF ")

모수 추정하기
TS2 <- arima(x, c(0, 0, 1))
TS2
##
## Call:
## arima(x = x, order = c(0, 0, 1))
##
## Coefficients:
## ma1 intercept
## 0.7655 -0.0508
## s.e. 0.0821 0.1907
##
## sigma^2 estimated as 1.176: log likelihood = -150.44, aic = 306.89
auto.arima(x)
## Series: x
## ARIMA(0,0,1) with zero mean
##
## Coefficients:
## ma1
## 0.7654
## s.e. 0.0821
##
## sigma^2 estimated as 1.189: log likelihood=-150.48
## AIC=304.96 AICc=305.08 BIC=310.17
모형의 진단
tsdiag(TS2,gof.lag=20)
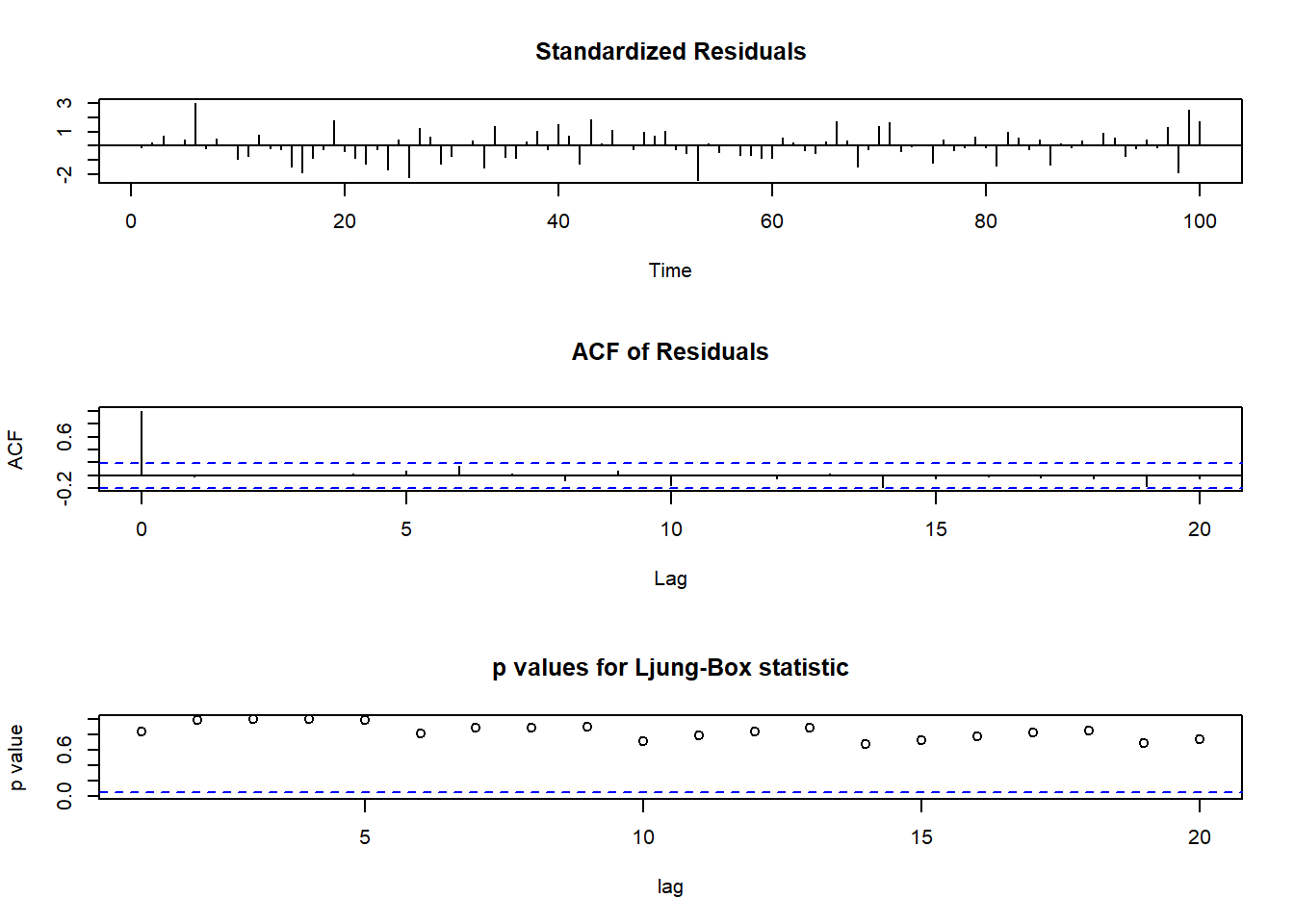
모형의 예측
future20<-predict(TS2, n.ahead=20)
future20
## $pred
## Time Series:
## Start = 101
## End = 120
## Frequency = 1
## [1] 1.38084893 -0.05080243 -0.05080243 -0.05080243 -0.05080243 -0.05080243
## [7] -0.05080243 -0.05080243 -0.05080243 -0.05080243 -0.05080243 -0.05080243
## [13] -0.05080243 -0.05080243 -0.05080243 -0.05080243 -0.05080243 -0.05080243
## [19] -0.05080243 -0.05080243
##
## $se
## Time Series:
## Start = 101
## End = 120
## Frequency = 1
## [1] 1.084481 1.365734 1.365734 1.365734 1.365734 1.365734 1.365734 1.365734
## [9] 1.365734 1.365734 1.365734 1.365734 1.365734 1.365734 1.365734 1.365734
## [17] 1.365734 1.365734 1.365734 1.365734
Upper <- future20$pred+future20$se
Lower <- future20$pred-future20$se
Upper
## Time Series:
## Start = 101
## End = 120
## Frequency = 1
## [1] 2.465330 1.314932 1.314932 1.314932 1.314932 1.314932 1.314932 1.314932
## [9] 1.314932 1.314932 1.314932 1.314932 1.314932 1.314932 1.314932 1.314932
## [17] 1.314932 1.314932 1.314932 1.314932
Lower
## Time Series:
## Start = 101
## End = 120
## Frequency = 1
## [1] 0.2963681 -1.4165366 -1.4165366 -1.4165366 -1.4165366 -1.4165366
## [7] -1.4165366 -1.4165366 -1.4165366 -1.4165366 -1.4165366 -1.4165366
## [13] -1.4165366 -1.4165366 -1.4165366 -1.4165366 -1.4165366 -1.4165366
## [19] -1.4165366 -1.4165366
forecast(TS2,h=20)
## Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
## 101 1.38084893 -0.008969209 2.770667 -0.7446945 3.506392
## 102 -0.05080243 -1.801061223 1.699456 -2.7275923 2.625987
## 103 -0.05080243 -1.801061223 1.699456 -2.7275923 2.625987
## 104 -0.05080243 -1.801061223 1.699456 -2.7275923 2.625987
## 105 -0.05080243 -1.801061223 1.699456 -2.7275923 2.625987
## 106 -0.05080243 -1.801061223 1.699456 -2.7275923 2.625987
## 107 -0.05080243 -1.801061223 1.699456 -2.7275923 2.625987
## 108 -0.05080243 -1.801061223 1.699456 -2.7275923 2.625987
## 109 -0.05080243 -1.801061223 1.699456 -2.7275923 2.625987
## 110 -0.05080243 -1.801061223 1.699456 -2.7275923 2.625987
## 111 -0.05080243 -1.801061223 1.699456 -2.7275923 2.625987
## 112 -0.05080243 -1.801061223 1.699456 -2.7275923 2.625987
## 113 -0.05080243 -1.801061223 1.699456 -2.7275923 2.625987
## 114 -0.05080243 -1.801061223 1.699456 -2.7275923 2.625987
## 115 -0.05080243 -1.801061223 1.699456 -2.7275923 2.625987
## 116 -0.05080243 -1.801061223 1.699456 -2.7275923 2.625987
## 117 -0.05080243 -1.801061223 1.699456 -2.7275923 2.625987
## 118 -0.05080243 -1.801061223 1.699456 -2.7275923 2.625987
## 119 -0.05080243 -1.801061223 1.699456 -2.7275923 2.625987
## 120 -0.05080243 -1.801061223 1.699456 -2.7275923 2.625987
plot(forecast(TS2,h=20))

실습3
ARMA<-arima.sim(list(ar=0.3, ma=0.7), n=100)
ts.plot(ARMA)
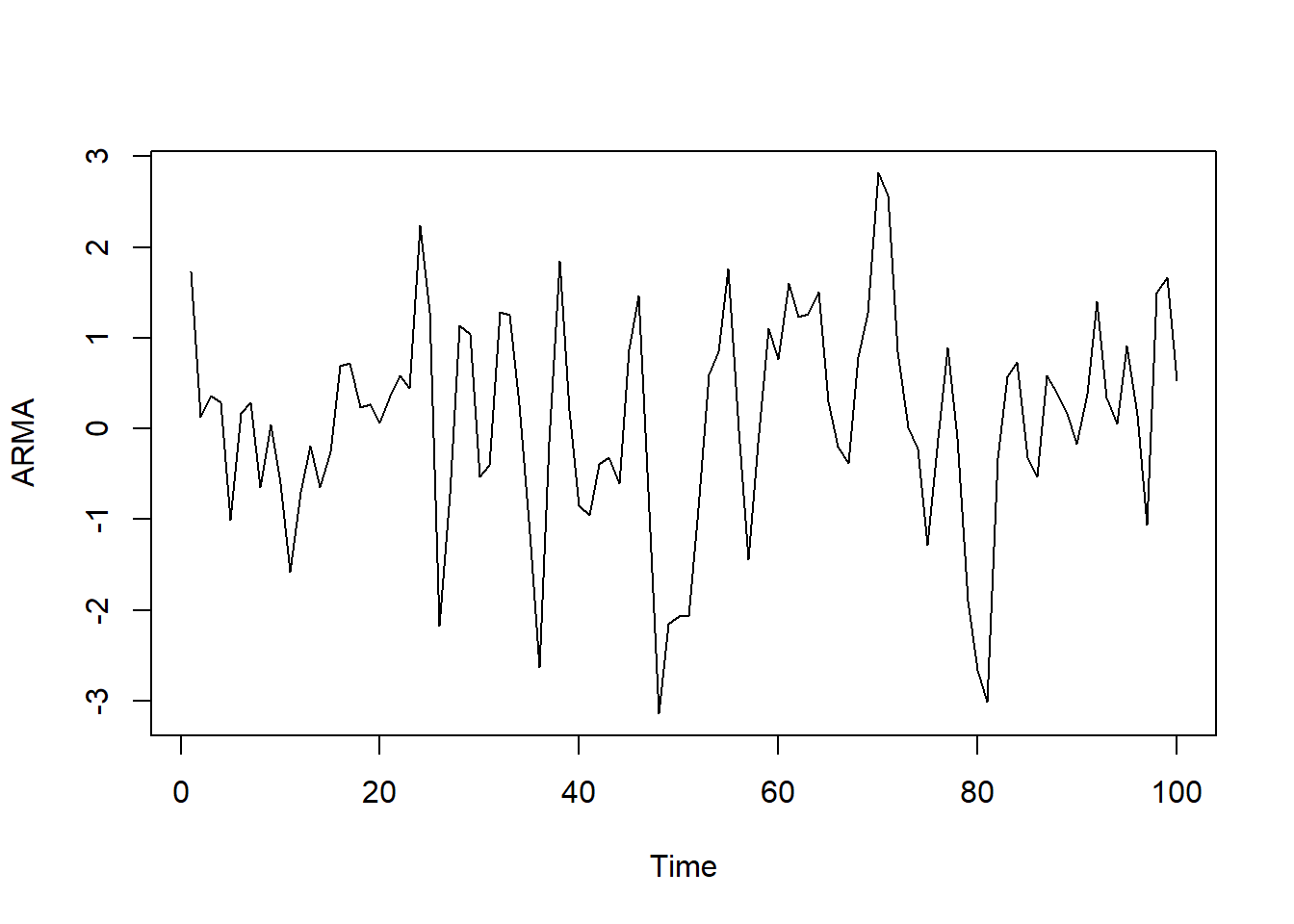
par(mfrow=c(1,2))
acf(ARMA)
pacf(ARMA)
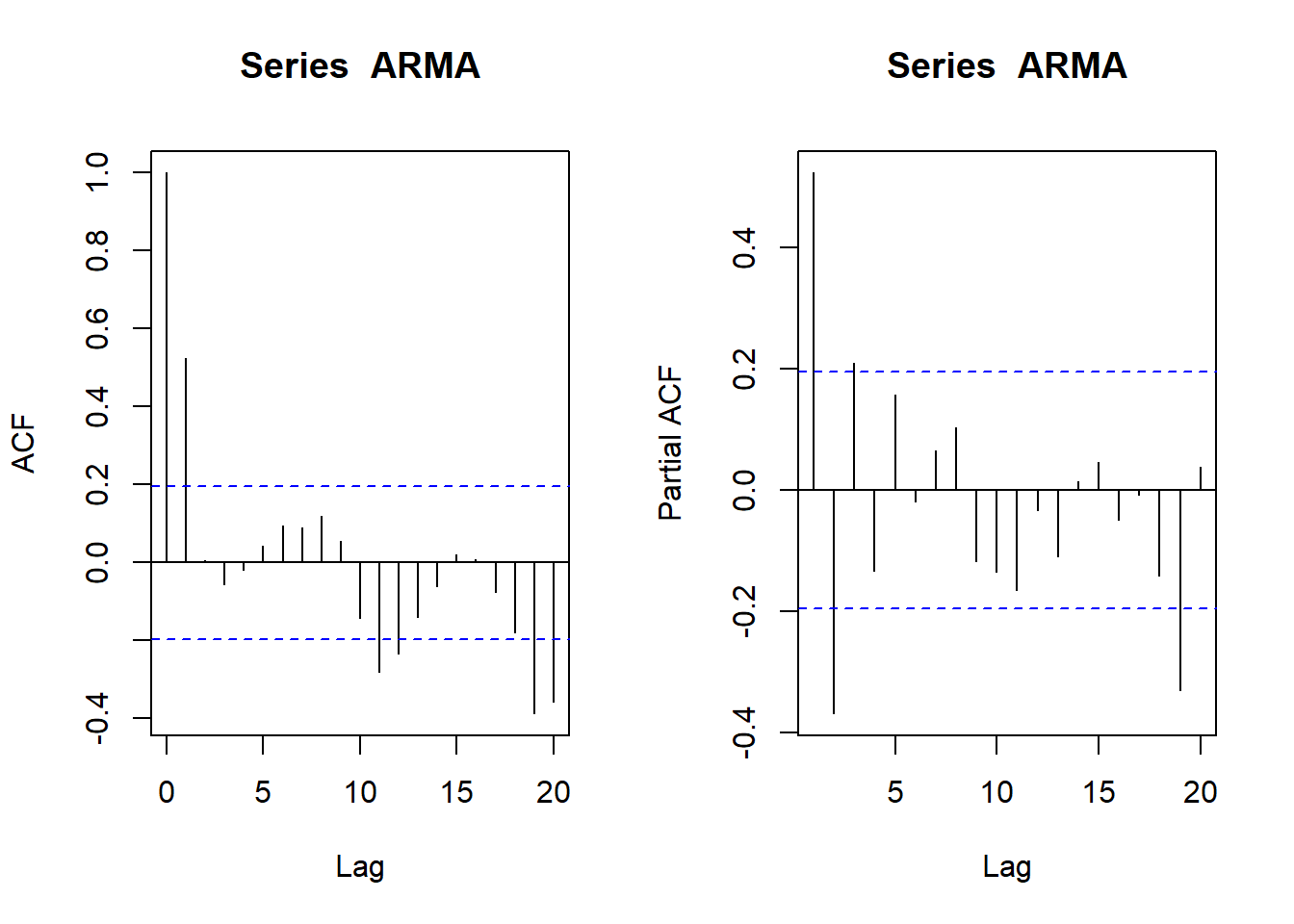
arm1 <- arima(ARMA, c(0, 0, 2))
arm1
##
## Call:
## arima(x = ARMA, order = c(0, 0, 2))
##
## Coefficients:
## ma1 ma2 intercept
## 0.9205 0.1859 0.0928
## s.e. 0.1134 0.1078 0.1828
##
## sigma^2 estimated as 0.7625: log likelihood = -128.83, aic = 265.67
arm2 <- arima(ARMA, c(1, 0, 1))
arm2
##
## Call:
## arima(x = ARMA, order = c(1, 0, 1))
##
## Coefficients:
## ar1 ma1 intercept
## 0.1761 0.6987 0.0925
## s.e. 0.1176 0.0737 0.1797
##
## sigma^2 estimated as 0.7689: log likelihood = -129.22, aic = 266.44
summary(arm1)
##
## Call:
## arima(x = ARMA, order = c(0, 0, 2))
##
## Coefficients:
## ma1 ma2 intercept
## 0.9205 0.1859 0.0928
## s.e. 0.1134 0.1078 0.1828
##
## sigma^2 estimated as 0.7625: log likelihood = -128.83, aic = 265.67
##
## Training set error measures:
## ME RMSE MAE MPE MAPE MASE
## Training set -0.008763483 0.8732173 0.6880229 88.86278 232.3577 0.7707185
## ACF1
## Training set -0.03455451
auto.arima(ARMA)
## Series: ARMA
## ARIMA(1,0,2) with zero mean
##
## Coefficients:
## ar1 ma1 ma2
## -0.6728 1.5869 0.7020
## s.e. 0.3673 0.3142 0.2212
##
## sigma^2 estimated as 0.765: log likelihood=-127.59
## AIC=263.17 AICc=263.6 BIC=273.6
tsdiag(arm1,gof.lag=36)
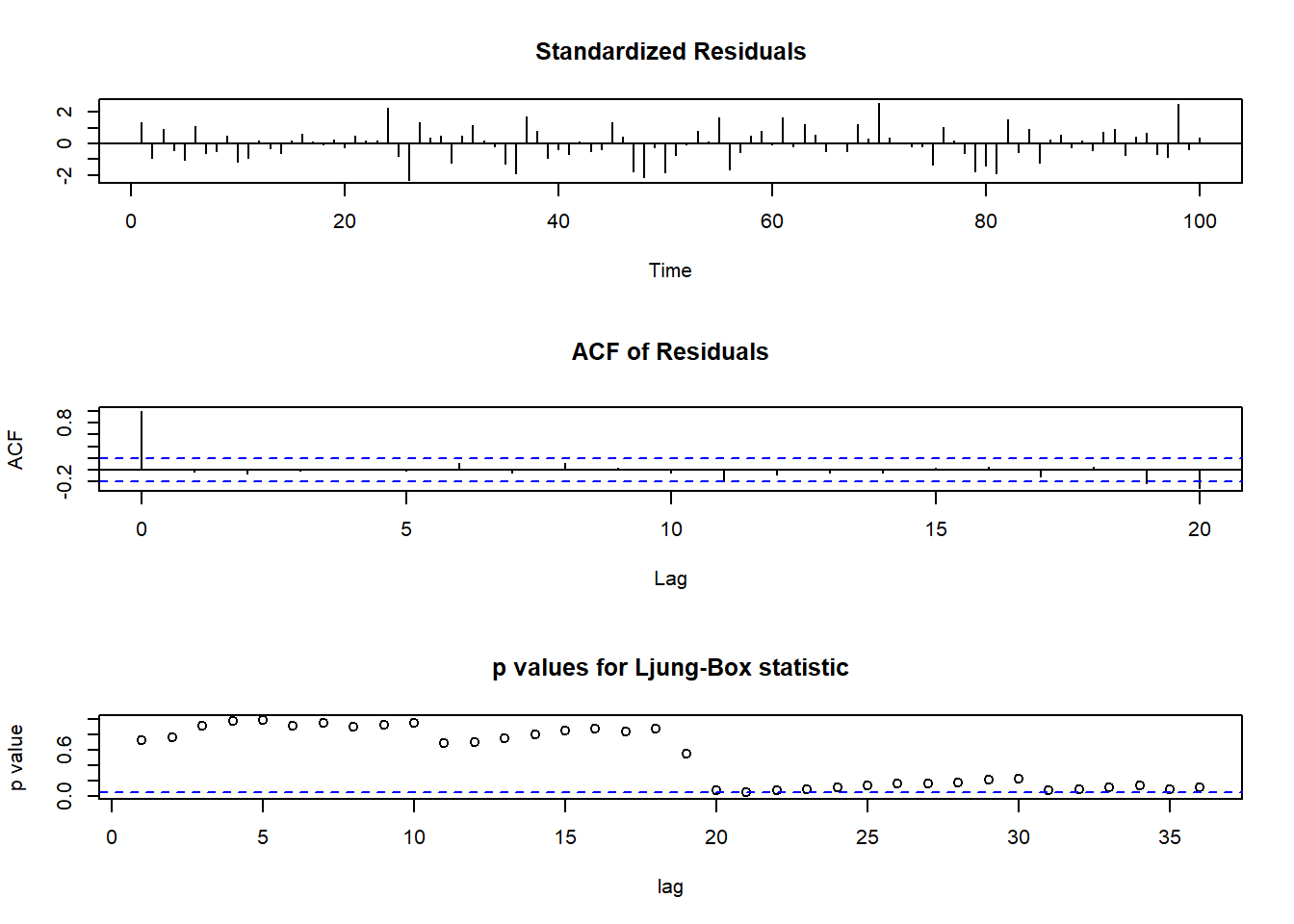
forecast(arm1,h=20)
## Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
## 101 0.32943030 -0.7896427 1.448503 -1.382044 2.040905
## 102 0.15210387 -1.3688593 1.673067 -2.174009 2.478216
## 103 0.09283052 -1.4422893 1.627950 -2.254933 2.440594
## 104 0.09283052 -1.4422893 1.627950 -2.254933 2.440594
## 105 0.09283052 -1.4422893 1.627950 -2.254933 2.440594
## 106 0.09283052 -1.4422893 1.627950 -2.254933 2.440594
## 107 0.09283052 -1.4422893 1.627950 -2.254933 2.440594
## 108 0.09283052 -1.4422893 1.627950 -2.254933 2.440594
## 109 0.09283052 -1.4422893 1.627950 -2.254933 2.440594
## 110 0.09283052 -1.4422893 1.627950 -2.254933 2.440594
## 111 0.09283052 -1.4422893 1.627950 -2.254933 2.440594
## 112 0.09283052 -1.4422893 1.627950 -2.254933 2.440594
## 113 0.09283052 -1.4422893 1.627950 -2.254933 2.440594
## 114 0.09283052 -1.4422893 1.627950 -2.254933 2.440594
## 115 0.09283052 -1.4422893 1.627950 -2.254933 2.440594
## 116 0.09283052 -1.4422893 1.627950 -2.254933 2.440594
## 117 0.09283052 -1.4422893 1.627950 -2.254933 2.440594
## 118 0.09283052 -1.4422893 1.627950 -2.254933 2.440594
## 119 0.09283052 -1.4422893 1.627950 -2.254933 2.440594
## 120 0.09283052 -1.4422893 1.627950 -2.254933 2.440594
plot(forecast(arm2,h=20))
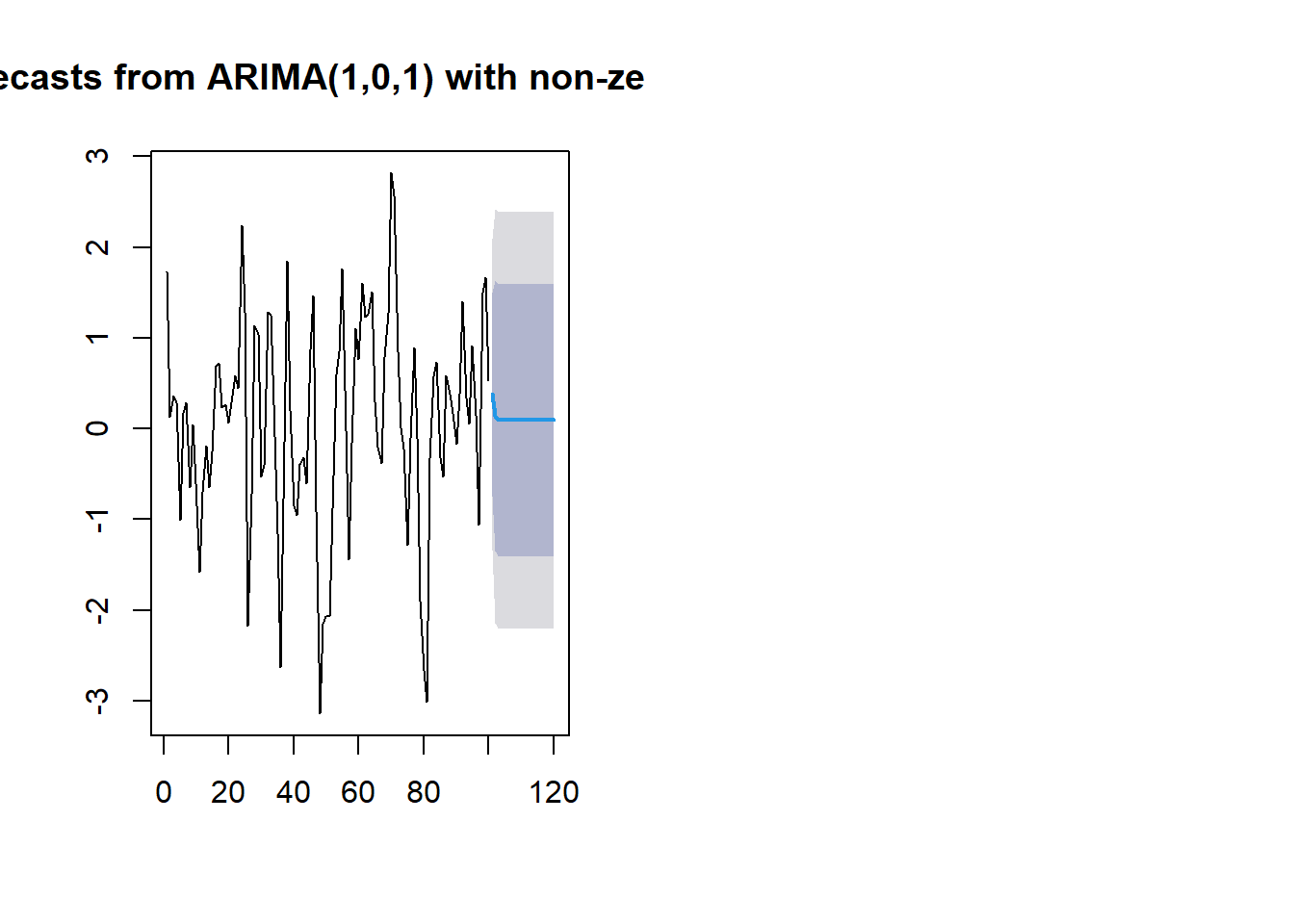
실습4
AirPassengers
## Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
## 1949 112 118 132 129 121 135 148 148 136 119 104 118
## 1950 115 126 141 135 125 149 170 170 158 133 114 140
## 1951 145 150 178 163 172 178 199 199 184 162 146 166
## 1952 171 180 193 181 183 218 230 242 209 191 172 194
## 1953 196 196 236 235 229 243 264 272 237 211 180 201
## 1954 204 188 235 227 234 264 302 293 259 229 203 229
## 1955 242 233 267 269 270 315 364 347 312 274 237 278
## 1956 284 277 317 313 318 374 413 405 355 306 271 306
## 1957 315 301 356 348 355 422 465 467 404 347 305 336
## 1958 340 318 362 348 363 435 491 505 404 359 310 337
## 1959 360 342 406 396 420 472 548 559 463 407 362 405
## 1960 417 391 419 461 472 535 622 606 508 461 390 432
plot(AirPassengers)
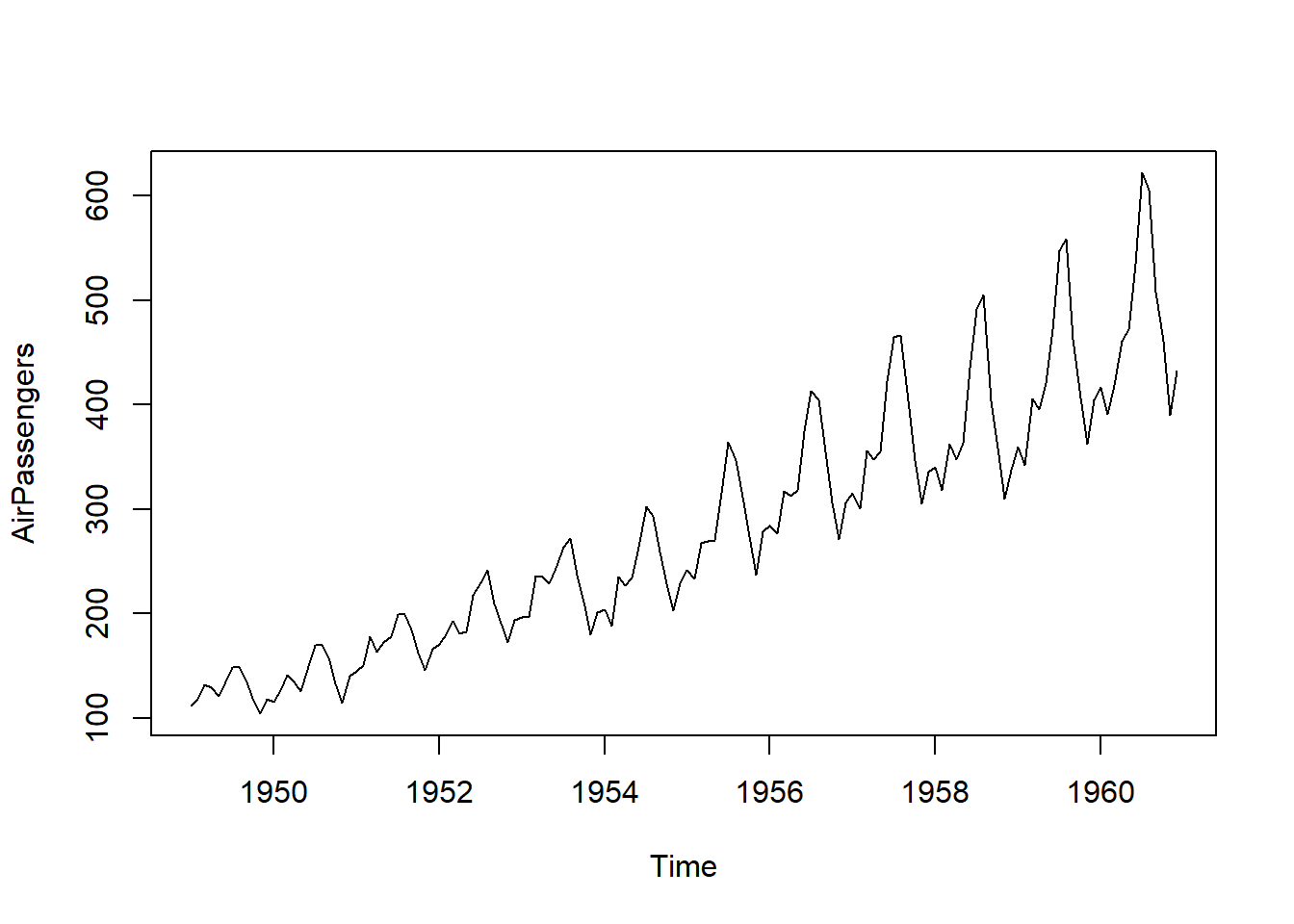
plot(stl(AirPassengers, s.window="periodic"))

logair<-log(AirPassengers)
plot(logair)
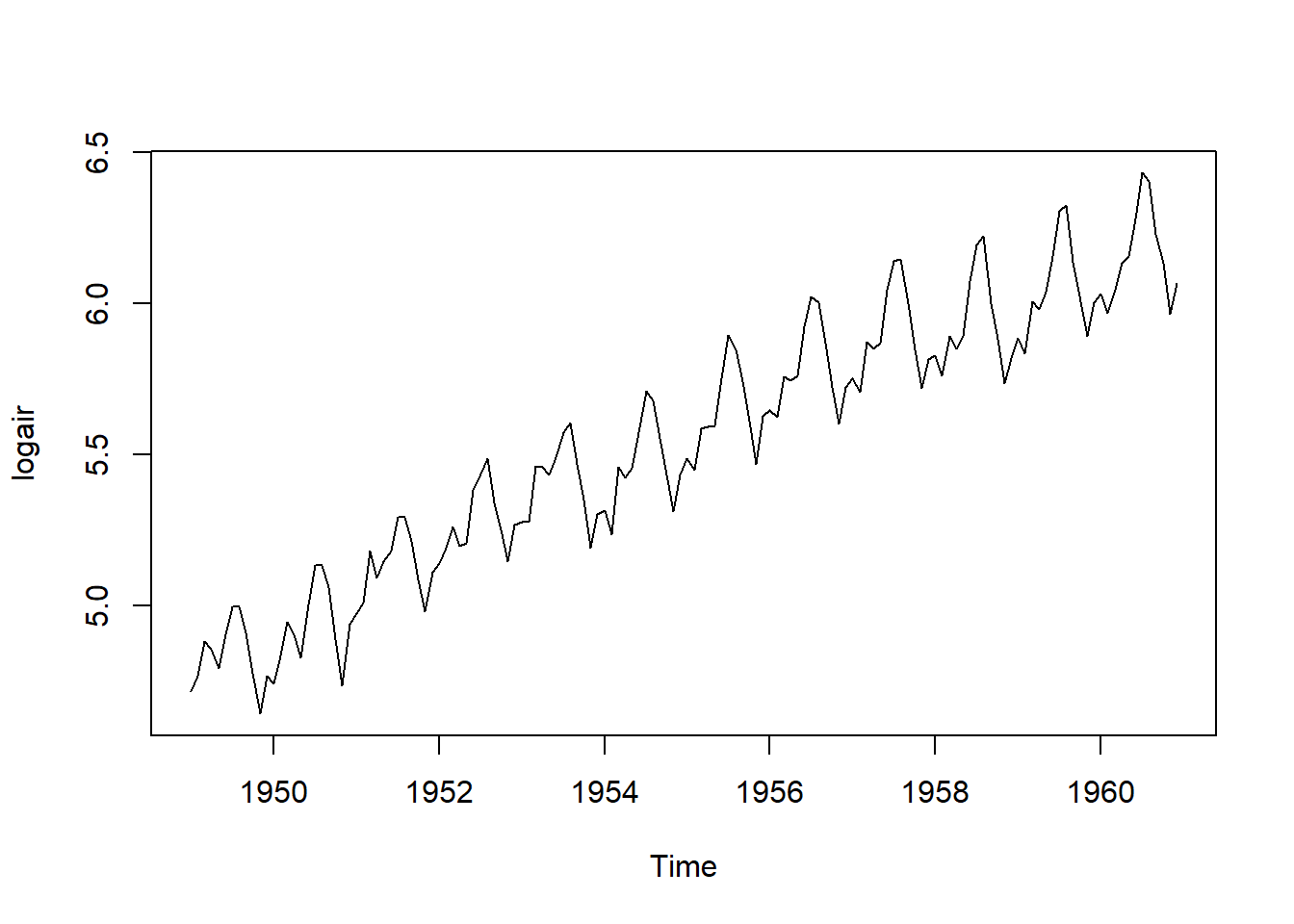
log_diff1_air<-diff(logair)
plot(log_diff1_air)
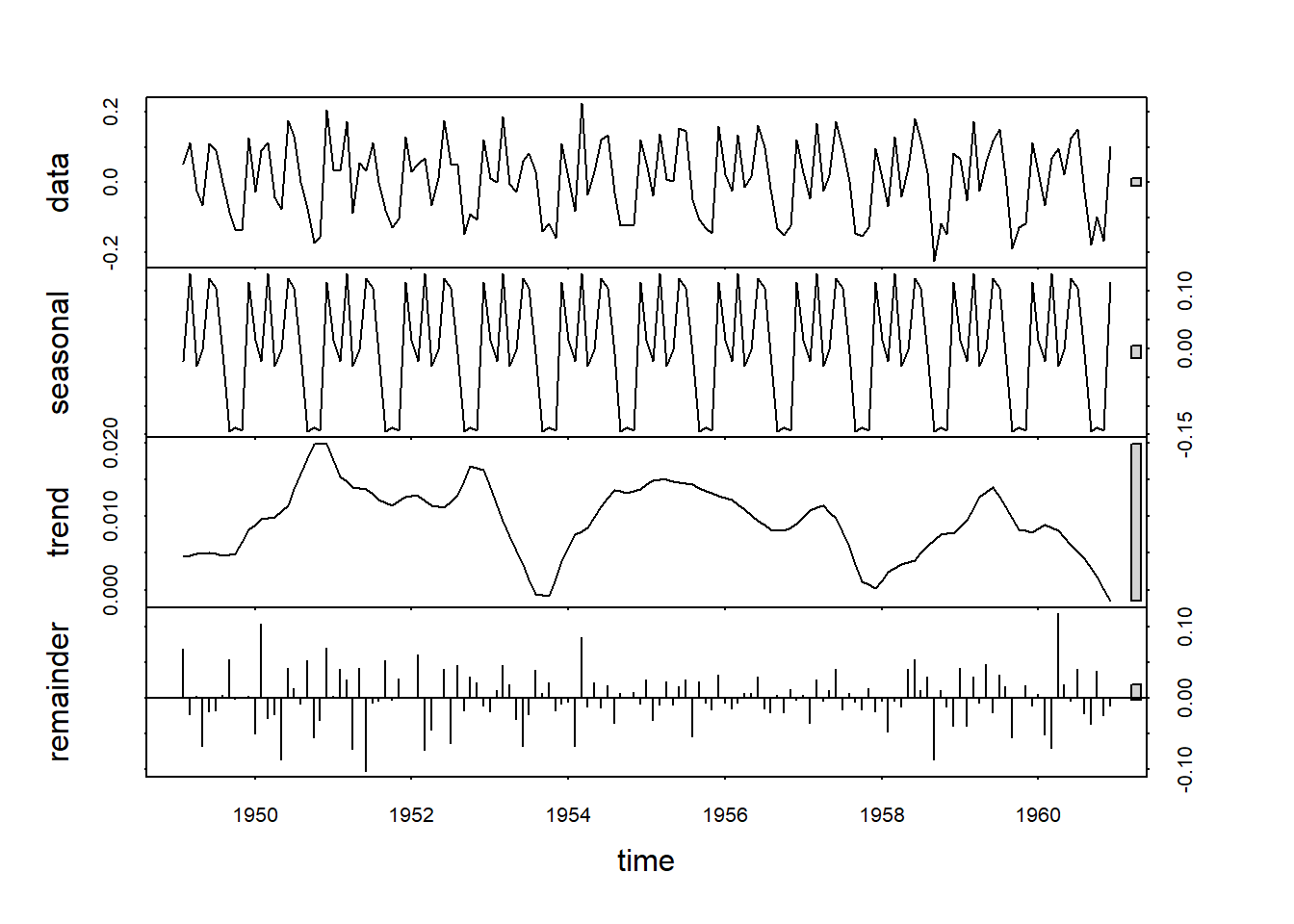
plot(stl(log_diff1_air, s.window="periodic"))
log_diff12_air<-diff(log_diff1_air, differences=12)
plot(log_diff12_air)
par(mfrow=c(2,1))
acf(log_diff12_air,main="ACF" )
pacf(log_diff12_air,main="PACF")
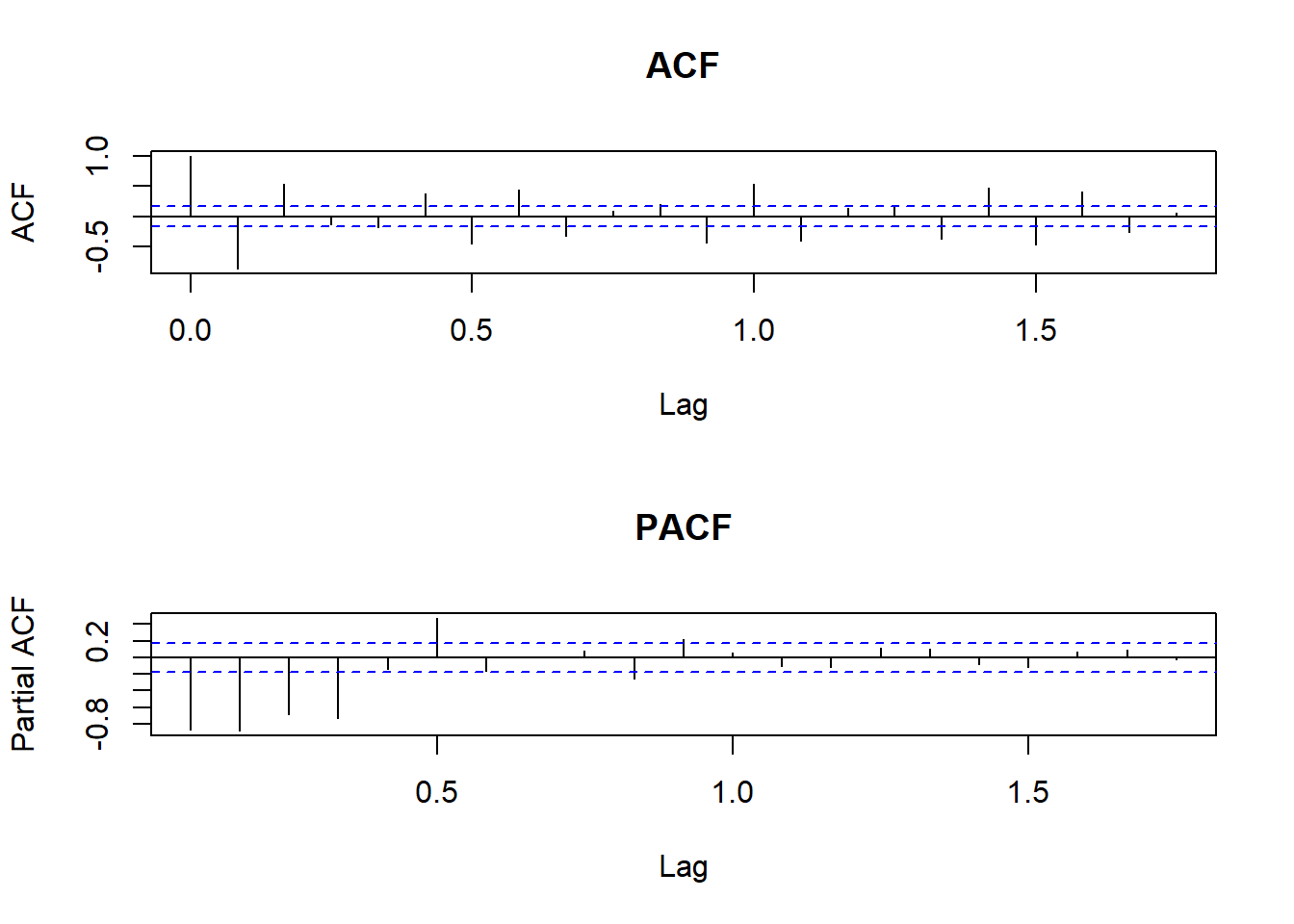
auto.arima(log_diff12_air)
## Series: log_diff12_air
## ARIMA(1,0,0)(2,0,0)[12] with zero mean
##
## Coefficients:
## ar1 sar1 sar2
## -0.9221 0.5517 0.2955
## s.e. 0.0294 0.0943 0.1040
##
## sigma^2 estimated as 1122: log likelihood=-652.39
## AIC=1312.78 AICc=1313.1 BIC=1324.28
tsdiag(auto.arima(diff(logair)))
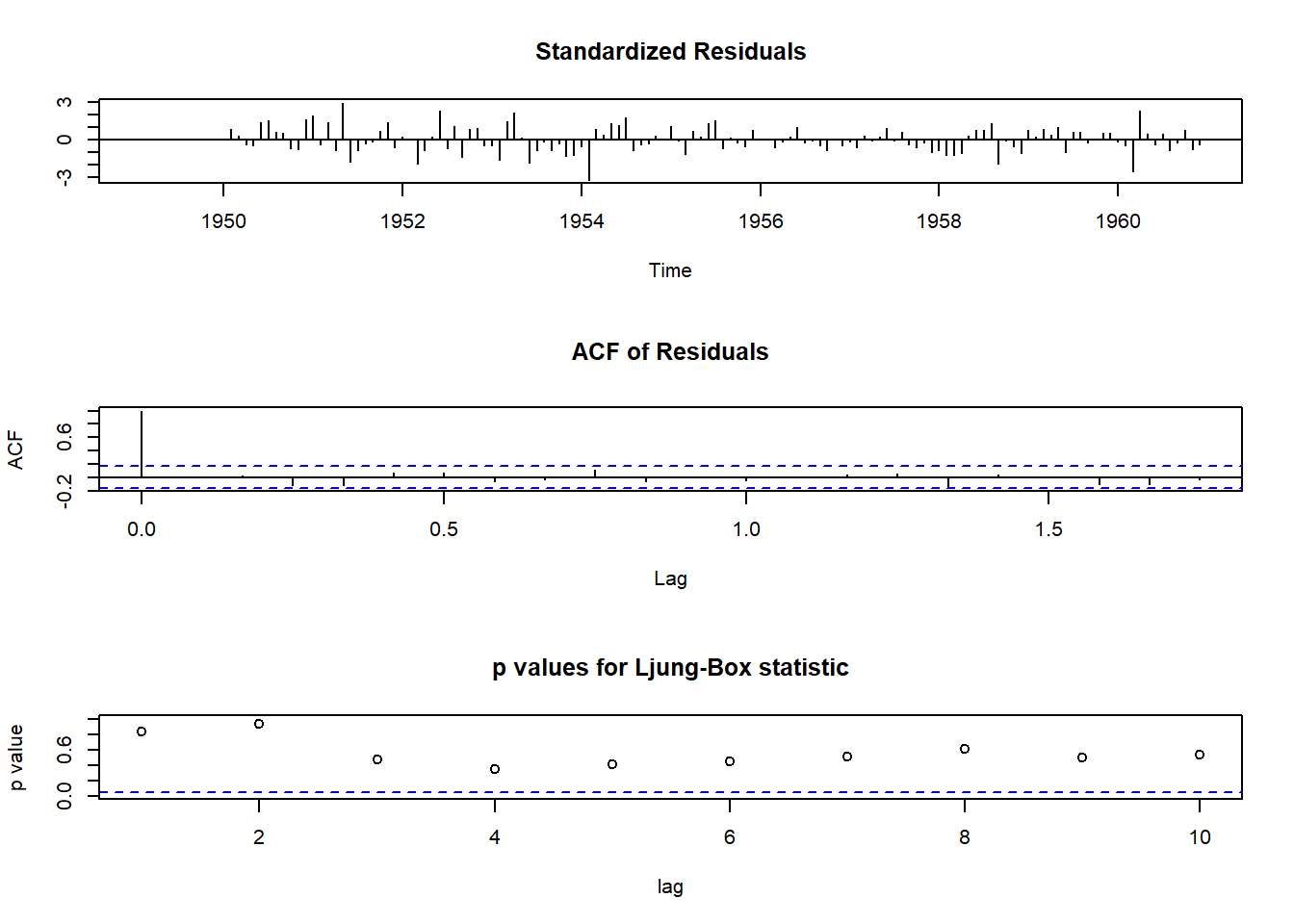
arm<-arima(logair,c(0,1,1), seasonal=list(order=c(0,1,1),period=12))
arm
##
## Call:
## arima(x = logair, order = c(0, 1, 1), seasonal = list(order = c(0, 1, 1), period = 12))
##
## Coefficients:
## ma1 sma1
## -0.4018 -0.5569
## s.e. 0.0896 0.0731
##
## sigma^2 estimated as 0.001348: log likelihood = 244.7, aic = -483.4
tsdiag(arm)

pred<-predict(arm, n.ahead=10*12)
pred
## $pred
## Jan Feb Mar Apr May Jun Jul Aug
## 1961 6.110186 6.053775 6.171715 6.199300 6.232556 6.368779 6.507294 6.502906
## 1962 6.206435 6.150025 6.267964 6.295550 6.328805 6.465028 6.603543 6.599156
## 1963 6.302684 6.246274 6.364213 6.391799 6.425054 6.561277 6.699792 6.695405
## 1964 6.398933 6.342523 6.460463 6.488048 6.521304 6.657526 6.796042 6.791654
## 1965 6.495183 6.438772 6.556712 6.584297 6.617553 6.753776 6.892291 6.887903
## 1966 6.591432 6.535022 6.652961 6.680547 6.713802 6.850025 6.988540 6.984153
## 1967 6.687681 6.631271 6.749210 6.776796 6.810051 6.946274 7.084789 7.080402
## 1968 6.783930 6.727520 6.845460 6.873045 6.906301 7.042523 7.181039 7.176651
## 1969 6.880180 6.823769 6.941709 6.969294 7.002550 7.138773 7.277288 7.272900
## 1970 6.976429 6.920019 7.037958 7.065544 7.098799 7.235022 7.373537 7.369150
## Sep Oct Nov Dec
## 1961 6.324698 6.209008 6.063487 6.168025
## 1962 6.420947 6.305257 6.159737 6.264274
## 1963 6.517197 6.401507 6.255986 6.360523
## 1964 6.613446 6.497756 6.352235 6.456773
## 1965 6.709695 6.594005 6.448484 6.553022
## 1966 6.805944 6.690254 6.544734 6.649271
## 1967 6.902194 6.786504 6.640983 6.745520
## 1968 6.998443 6.882753 6.737232 6.841770
## 1969 7.094692 6.979002 6.833481 6.938019
## 1970 7.190941 7.075251 6.929731 7.034268
##
## $se
## Jan Feb Mar Apr May Jun
## 1961 0.03671562 0.04278291 0.04809072 0.05286830 0.05724856 0.06131670
## 1962 0.09008475 0.09549708 0.10061869 0.10549195 0.11014981 0.11461854
## 1963 0.14650643 0.15224985 0.15778435 0.16313118 0.16830825 0.17333075
## 1964 0.20896657 0.21513653 0.22113442 0.22697386 0.23266679 0.23822371
## 1965 0.27748210 0.28408309 0.29053414 0.29684503 0.30302451 0.30908048
## 1966 0.35174476 0.35876289 0.36564634 0.37240257 0.37903840 0.38556004
## 1967 0.43142043 0.43883816 0.44613258 0.45330963 0.46037481 0.46733319
## 1968 0.51620376 0.52400376 0.53168935 0.53926541 0.54673651 0.55410688
## 1969 0.60582584 0.61399203 0.62205103 0.63000694 0.63786363 0.64562471
## 1970 0.70005133 0.70856907 0.71698563 0.72530453 0.73352910 0.74166246
## Jul Aug Sep Oct Nov Dec
## 1961 0.06513124 0.06873441 0.07215787 0.07542612 0.07855851 0.08157070
## 1962 0.11891946 0.12307018 0.12708540 0.13097758 0.13475740 0.13843405
## 1963 0.17821177 0.18296261 0.18759318 0.19211216 0.19652727 0.20084534
## 1964 0.24365393 0.24896574 0.25416656 0.25926308 0.26426132 0.26916676
## 1965 0.31502004 0.32084967 0.32657525 0.33220217 0.33773535 0.34317933
## 1966 0.39197318 0.39828307 0.40449455 0.41061207 0.41663978 0.42258152
## 1967 0.47418947 0.48094803 0.48761291 0.49418791 0.50067658 0.50708223
## 1968 0.56138049 0.56856106 0.57565206 0.58265678 0.58957827 0.59641945
## 1969 0.65329361 0.66087351 0.66836746 0.67577831 0.68310877 0.69036139
## 1970 0.74970759 0.75766731 0.76554426 0.77334099 0.78105989 0.78870326
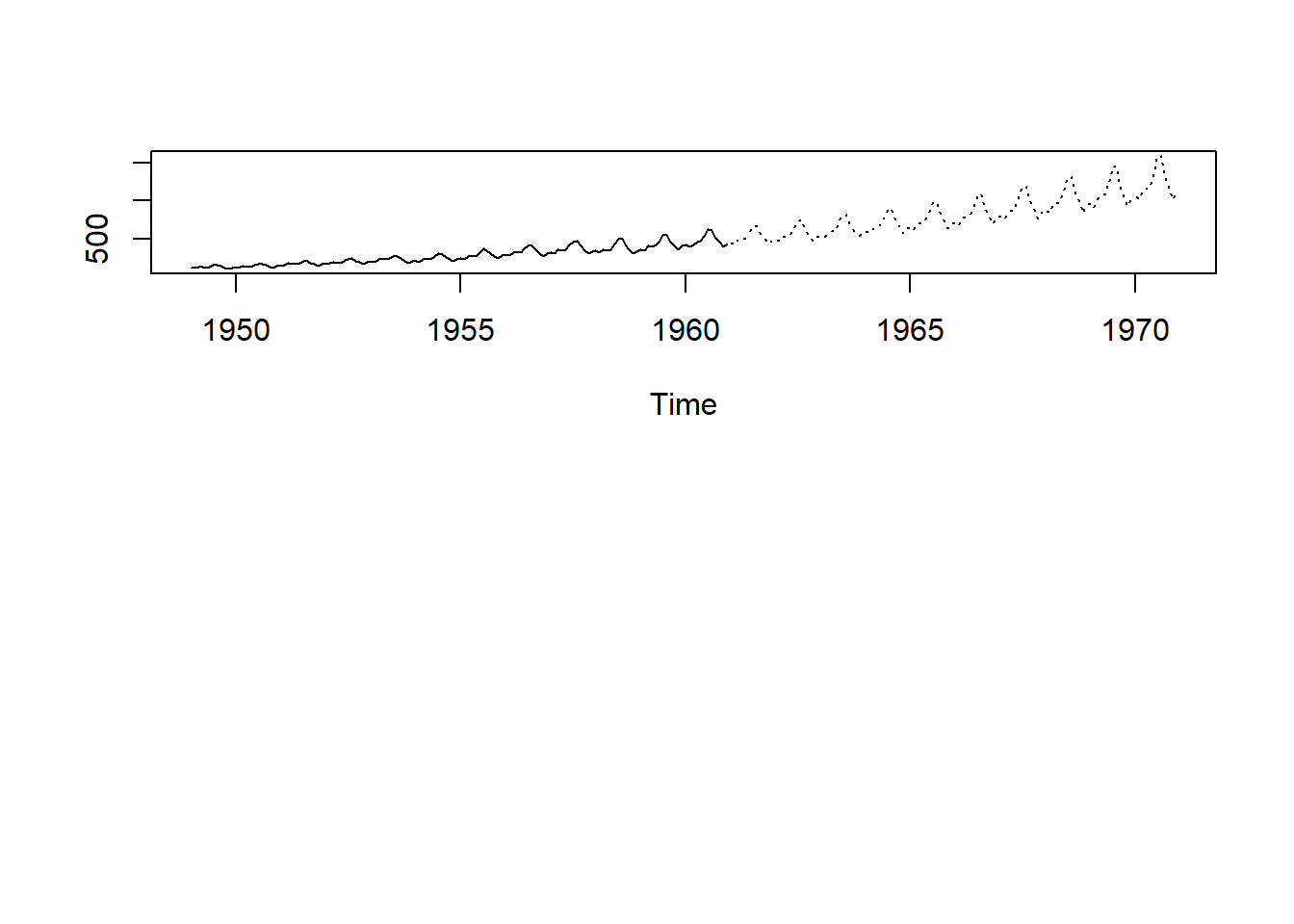
zz <- ts.plot(AirPassengers, 2.718^pred$pred, lty=c(1,3))
zz
## NULL